Is Larger Better in Particle Physics?
How particle accelerators retrace the course of time.

Since the discovery of X-rays and radioactivity at the turn of the 20th century, the beams of particles opened us new horizons that our eyes couldn’t contemplate before. From the first radiograph in 1895 to the discovery of the Higgs boson in 2012, many breakthroughs in modern physics are tightly connected to the development of particle accelerators. For research in fundamental physics, these machines generate beams of charged particles with precise parameters under control continuously. They have, however, a clear tendency to grow drastically in size at every new generation.
The first modern particle accelerator built by Ernest Lawrence at the beginning of the 30s was only a few centimetres wide, and it could fit in your hand. Today, the largest accelerator in the world, the Large Hadron Collider (LHC) at CERN is a ring of 27 km located 100 meters underground. You can fit several billions of Lawrence’s accelerator inside the LHC ring. Quite an impressive jump in 90 years and it’s not the end. The next generation currently studied, called the Future Circular Collider (FCC), is expected to be four times larger than the LHC, using technologies that don’t exist today. Why are physicists doing this? To uncover the mysteries of the Universe, of course!
Particle Accelerators for Pedestrians
A particle accelerator can be linear or circular. It constrains beams of charged particles on a trajectory to … accelerate them. Joke aside, particles are accelerated naturally like in the process of radioactive decay or the cosmic rays. We receive particles from space with an energy that we cannot even dream of achieving (yet?) on earth. What makes the particle accelerators unique is the reproducibility. You control all parameters of the experiment, and you can make it again and again to confirm your theory. That’s what we do in science, right? Notice also that particle accelerators are also widely used in the industry (e.g. food products sterilisation) or for medical applications (e.g. cancer treatment).
The principle behind these machines is well established since the birth of the discipline. An electric field kicks the particles, increasing their energy, and a magnetic field holds the particles inside the accelerator. So, the possibility to reach higher energy relies mainly on our ability to generate stronger electric and magnetic fields. Nevertheless, these technologies don’t evolve as fast as we would like, and we need to make sacrifices on the size of the accelerators.
Imagine, you have a piece of equipment with a substantial electric field at your disposal, but it’s not sufficient to accelerate the particle to the energy you want in one go. What can you do?
- Pile several of them up linearly to reach the energy.
- Make particles turn around to pass multiply times in the equipment.
In the first case, the length of the accelerator increases with the energy you want to obtain. In the second case, you must use a magnetic field to bend the particle trajectory. This magnetic field cannot be arbitrarily large, which constrains the size of the ring. The larger the energy of the particles, the larger the radius of the trajectory, as you can see in the drawing below.
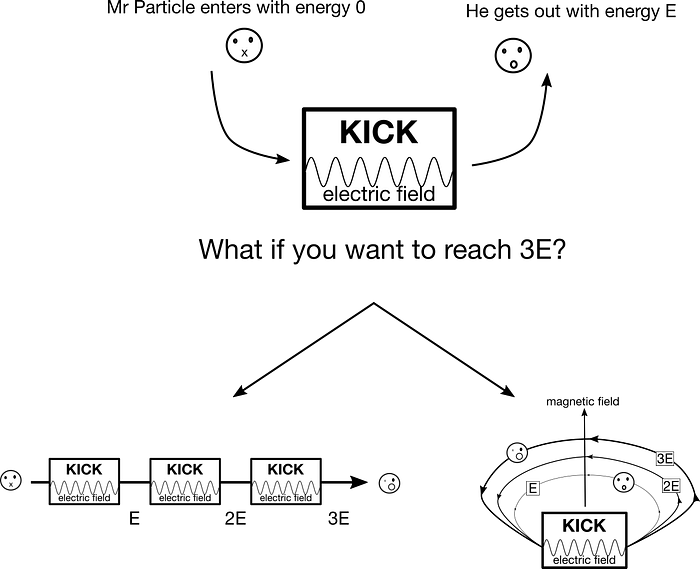
This is an extremely simplified view but you get the idea. In reality we use a chain of different accelerators to reach very high energy. It is the case for the LHC. If you want to get more familiar with the design of accelerators, I encourage you to watch this record from a CERN lecture. You can also navigate on the CERN Accelerator School website and search for lecture proceedings.
The LHC is a machine of all the superlatives. Colder and emptier than the intergalactic space. Collisions are happening at temperatures thousands of time hotter than the centre of the sun. It’s also fairly ranked in the list of most expensive scientific experiments of all time. All this to produce particle beams with higher energy. So why? What do physicists hope to discover with these gigantic apparatus?
Mass is Energy and Vice Versa
There is an equation that everybody knows. Maybe the most simple but powerful equation ever written.
It tells you that mass and energy are equivalent. Mass can be created out of thin air if you provide energy. Mass can disappear, releasing energy. As chemists are saying « Nothing is lost, nothing is created, everything is transformed ». Einstein and its equation said: Yes, and everything is energy. In a nutshell, the Einstein equation paved the way for the quest of particles with always higher energy in our particle accelerators.
In particle physics the energy is generally measured in electron-volt (eV). Not in Joule or Calories like in your everyday life. While your body needs millions of Joule in a day, the energy exchanged in elementary particle interactions are far far smaller. Two eV is 19 orders of magnitude smaller than a Joule. Still, it corresponds to the energy of the sunlight photons striking the earth. That’s the kind of energy scale that we manipulate in particle physics.
The mass of a particle itself can be expressed in eV according to Einstein’s equation (omitting the speed of light for simplicity). The mass of an electron is 0.5 MeV (mega-electron-volt), the one of a proton is 1 GeV (giga-electron-volt). The mass of all the elementary particles are ranging from 0 (the photon has no mass) to more than 150 GeV. If you want to materialise one of these particles, you need to bring at least its mass energy. And that’s what physicists do!
In short, to study the standard model of particle physics, you accelerate particles easily available like protons or electrons. Then you make the beam collide with either a fixed target (like a metal foil) or a second beam. If there is enough energy, other particles may appear for a short time and disintegrate in different particles. Don’t forget to place detectors around the collision point to observe what happened. Do it for a long period and collect a sufficient amount of data. You can then verify if it agrees with your theory. That’s the idea.
There is undoubtedly much more to say. Experiments with a fixed target are generally here to study the target. You can study new material, how its atoms are arranged, for example. When you make two beams collide, the accelerator is called a collider (like the LHC). It’s generally used to study fundamental physics since the collision energy sums. The accelerator physics is certainly very appealing, but there is a second fascinating aspect of these gigantic atoms smasher.
A Particle Accelerator Is a Microscope
The bestiary of particle physics is vast and captivating. The theory of fundamental physics is so robust that no experiment has been able to invalidate it. Physicists predicted the existence of particles with fancy names. Pions, Kaons, charming and exotic particles, there is even a particle called gipsy (J/Ψ). All of them were observed in beam collisions, assuming these beams had enough energy. There is, however, an even more crucial aspect for the pursuit of higher energies. The larger the energy, the deeper you can explore the realm of the infinitely small. It transforms a particle accelerator into a microscope.
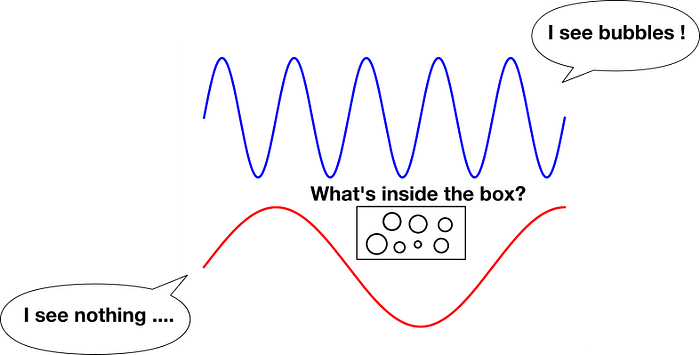
How is this possible? There are two ways of picturing this. First, when you think about electromagnetic waves (like sunlight). Higher energy means a shorter wavelength, and this wave can distinguish smaller details. See the illustration below. You can feel that the shorter wave (higher energy) can see what is inside the box. The largest one (smaller energy) will see just a box and no detail of what it contains.
The modern physics picture gives a second approach. Particles mediate all interactions. Take a simple interaction like two electrons (e⁻) in motion, bouncing on each other (this is called the scattering of two electrons). They interact through their electric field, which is mediated by the photon (γ). Physicists represent interactions using Feynman diagram (see the figure below). The x-axis corresponds to the time, the two electrons come in, they interact through the photon, and they drift away. This photon, however, is special. It exists during such a short time that it’s impossible to detect it. It’s not a problem with our detectors. It’s really impossible to see it. Physicist call this kind of particle, a virtual particle.
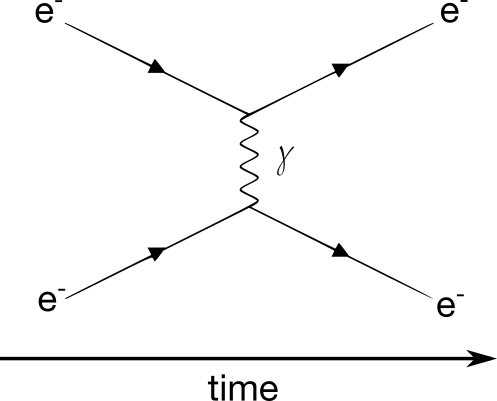
The virtual particle is a weird feature of the theory, but it satisfies the Heisenberg uncertainty principle. In mathematical term, it means its lifetime is inversely proportional to its energy. The larger the energy, the smaller the life of the particle and therefore, the shorter distance it can travel (it can’t go faster than the speed of light). We can conclude that with larger energy, we can observe phenomenons happening on shorter distances. We can see smaller details, like with a microscope. But that’s not all.
Accelerator Are Time Machines
The Big Bang theory uncovered an even more compelling motive to increase the energy in our particle accelerators. Higher energy collisions allow getting back in time, closer the first instants of the cosmos. The baby universe was a hot dense plasma where no atom we observe today could exist. It took 380’000 years to the universe to cool down enough to let the atoms of helium and hydrogen form. At this very moment, the light was free to move without being absorbed by surrounding electrons.
We can contemplate today this first snapshot of the primitive universe. It’s what we call the Cosmic Microwave Background (CMB). It’s, however, impossible to observe the universe before this moment with our telescopes since the light was not free to move. Particle accelerators allow seeing across the wall of the CMB.
Thermodynamic considerations of the primordial plasma link the temperature of the plasma with the age of the early universe. The temperature is a macroscopic quantity representing the energy of the collisions in a box of particles. Take your kettle, when you switch it on, you increase the agitation of the water molecules inside. When the temperature reaches 100°C, the molecules have enough excitation to jump off the kettle in large quantity, and you see the steam.
You can translate this to define the temperature of a plasma and, therefore, link the age of the universe with the collision energy. The result is that the time of the early universe is inversely proportional to the square of the collision energy. I show below a timeline of the first 380'000 years of the universe and the corresponding collision energy.
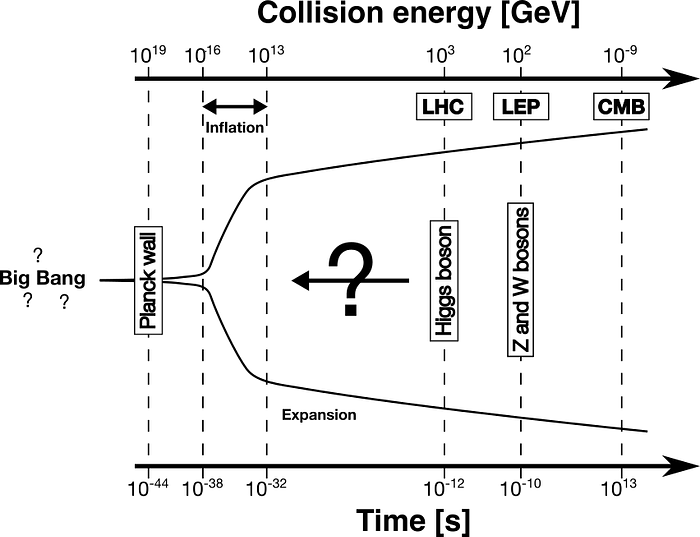
I included where we are now with the LHC and the discovery of the Higgs boson. I mention as well the LEP (Large Electron-Positron Collider), the predecessor of the LHC which studied in great detail mechanisms involving the Z and W bosons. As you can see, there is still a lot of room for improvement to reach the first instant of the cosmos, before the cosmic inflation. If one day we ever touch the Planck wall, our vision of the fundamental laws of Nature may have changed drastically. Our models of particle physics and cosmology still contain unanswered questions. However, particle accelerators play and will play a crucial role in our quest to understand the origin of everything.
If you are still wondering why research centres like CERN are essential for society in general, don’t forget that scientists there invented the World Wide Web as you know it today to boost collaboration. Just this fact alone should be sufficient to support our need for fundamental research. It spurs the development of cutting-edge technology with many applications far beyond science itself.
To Go Further
- Particle Accelerators: From Big Bang Physics to Hadron Therapy, U. Amaldi, 2015. This book will give you a panorama of the history of particle accelerators and the research associated.
- https://home.cern/science/accelerators/large-hadron-collider. If you want to know more about the LHC, the CERN website is always a good source.
- The Multi-Universe Cosmos, The First Complete Story of the Origin of the Universe, A.K. Velan, 1992. This book gives you a complete introduction to the physics of elementary particles and cosmology, also expanding your mind to physics beyond the standard model.
